Daily Practice
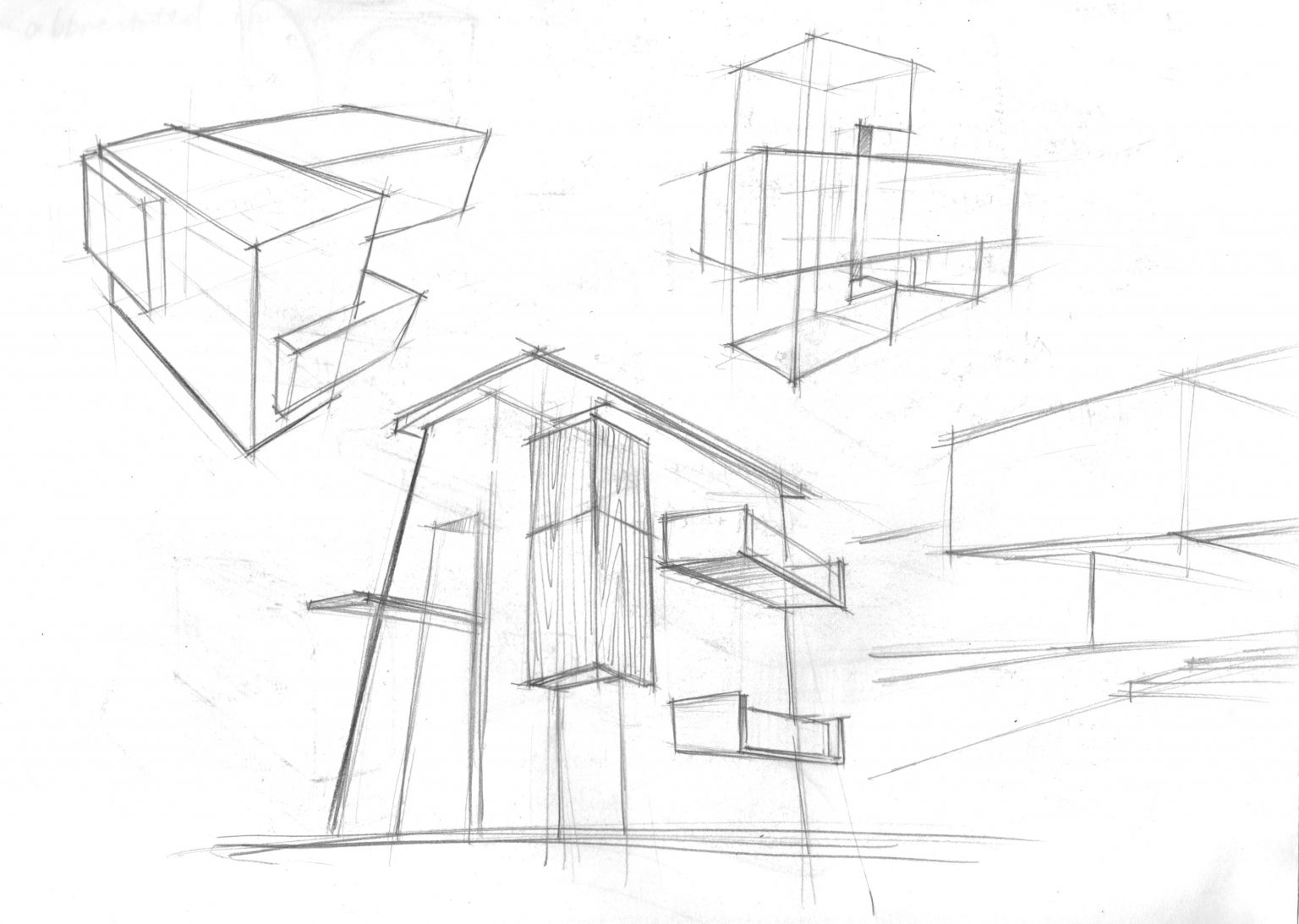
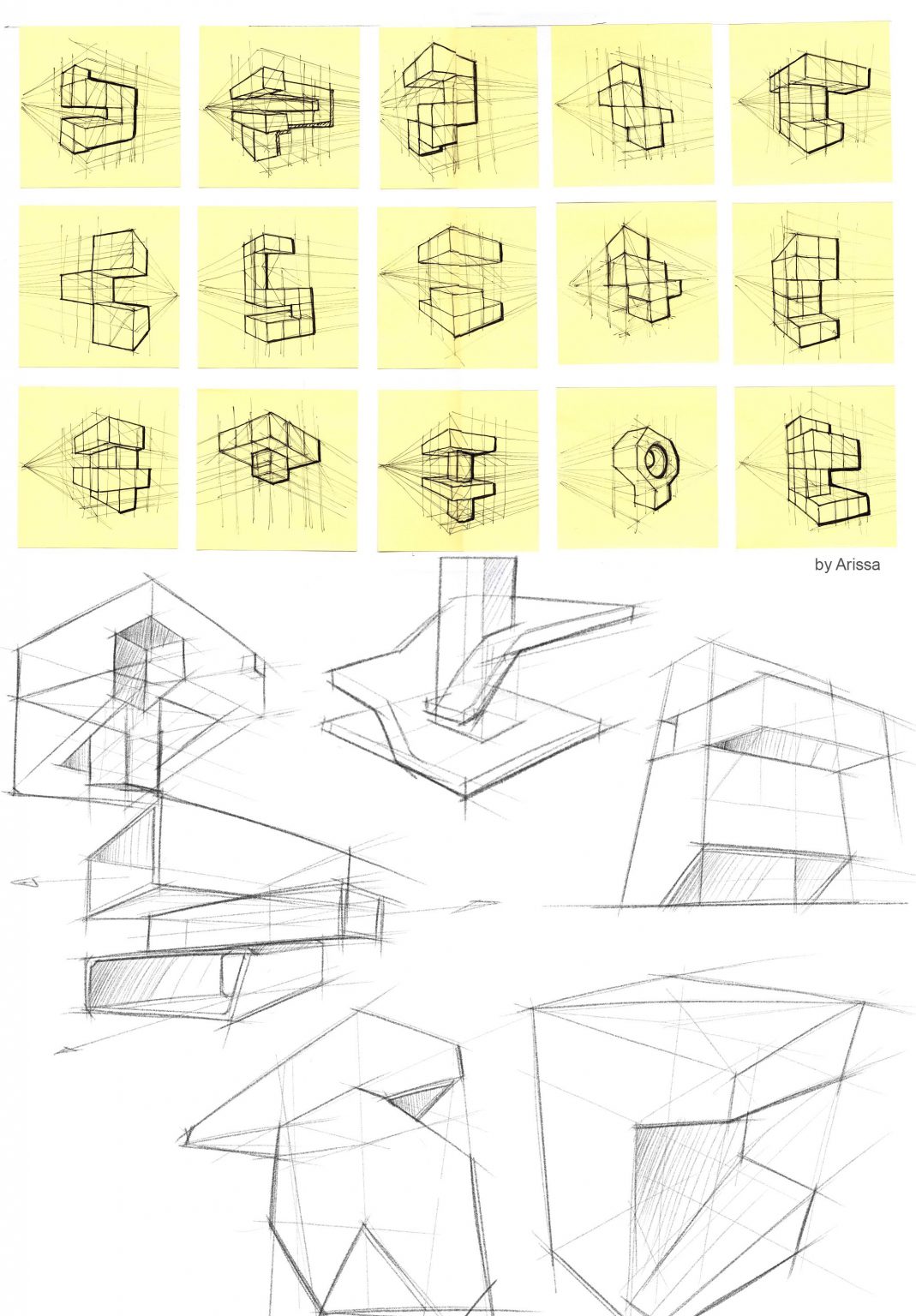
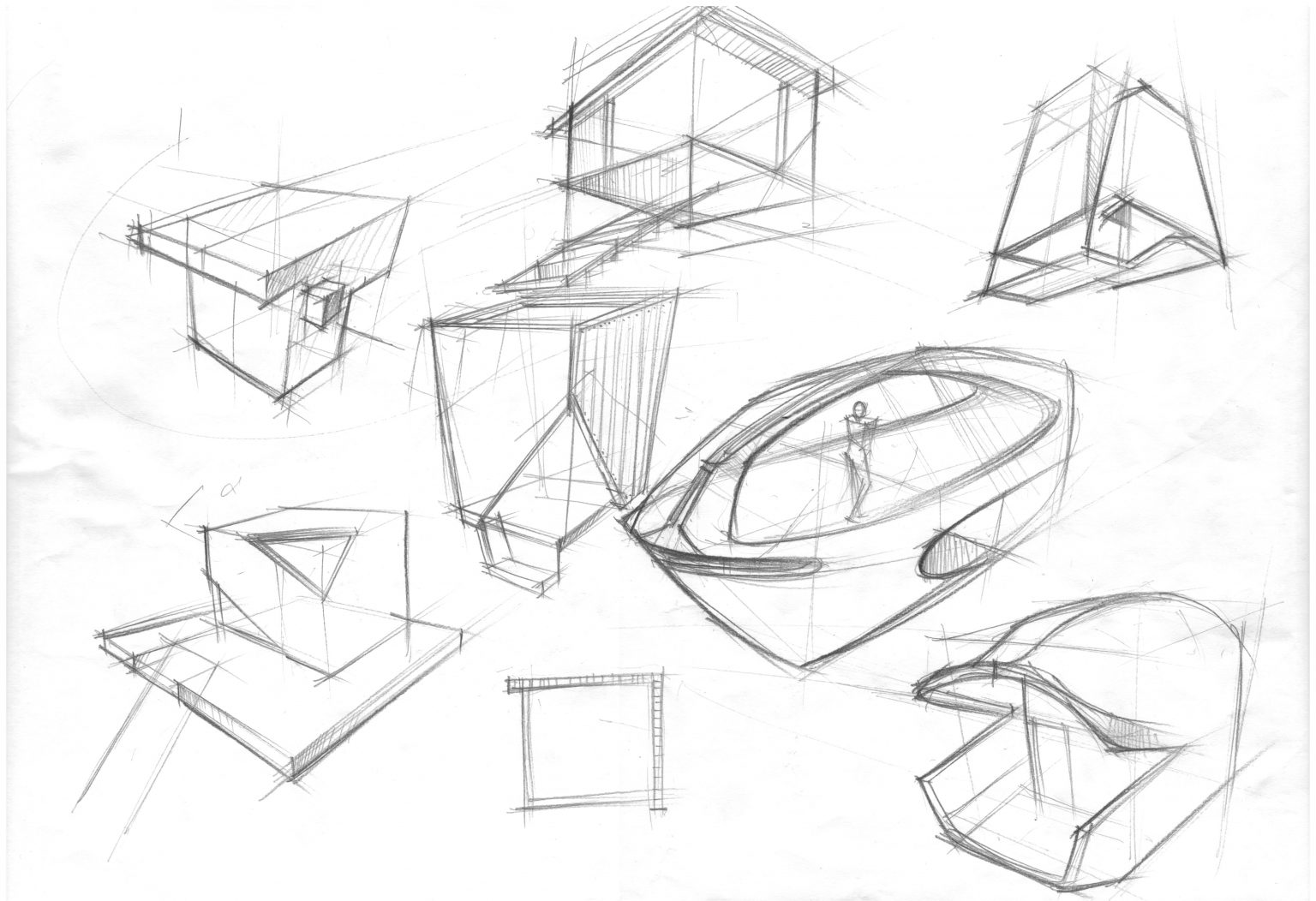
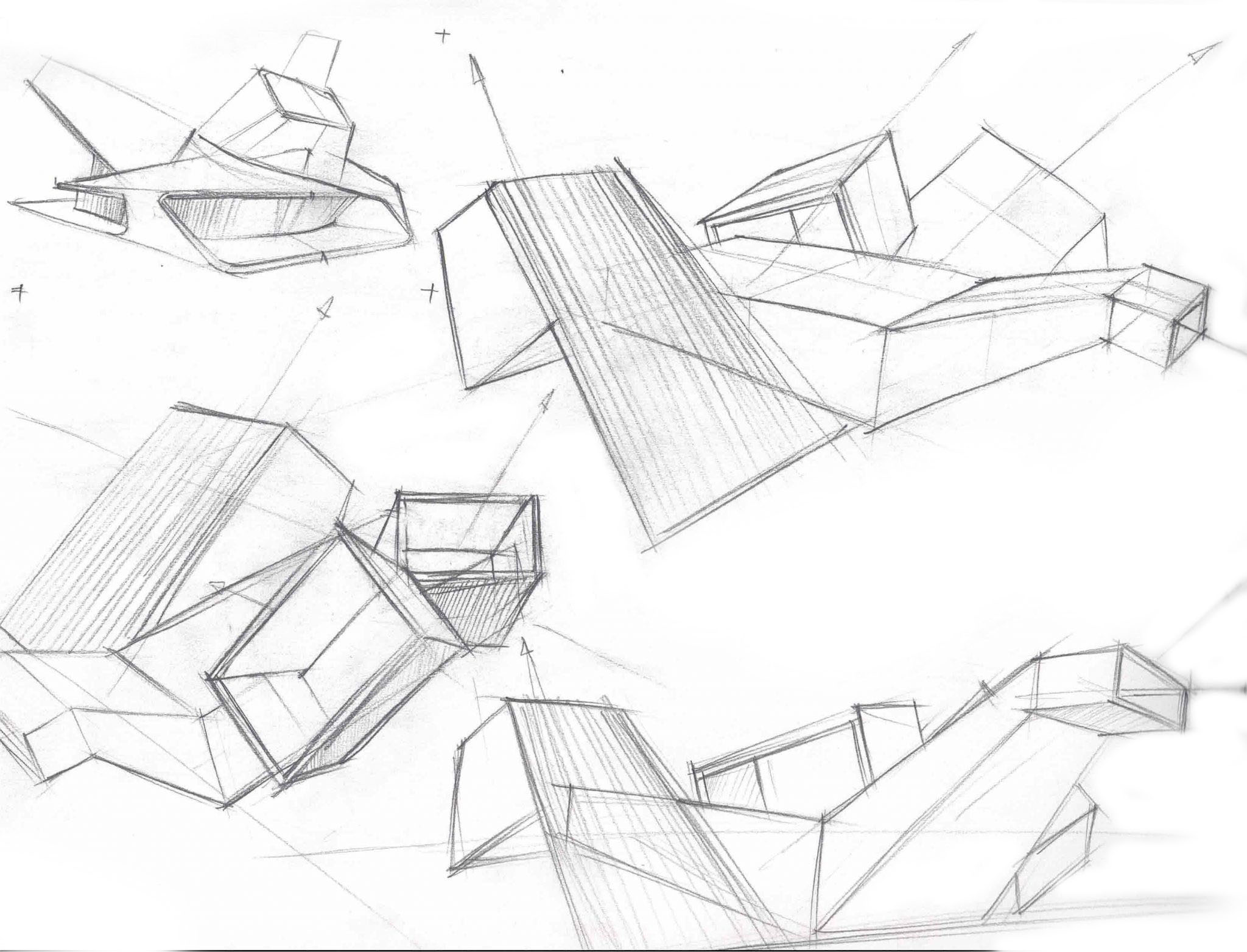
Primitive Drawing Practice
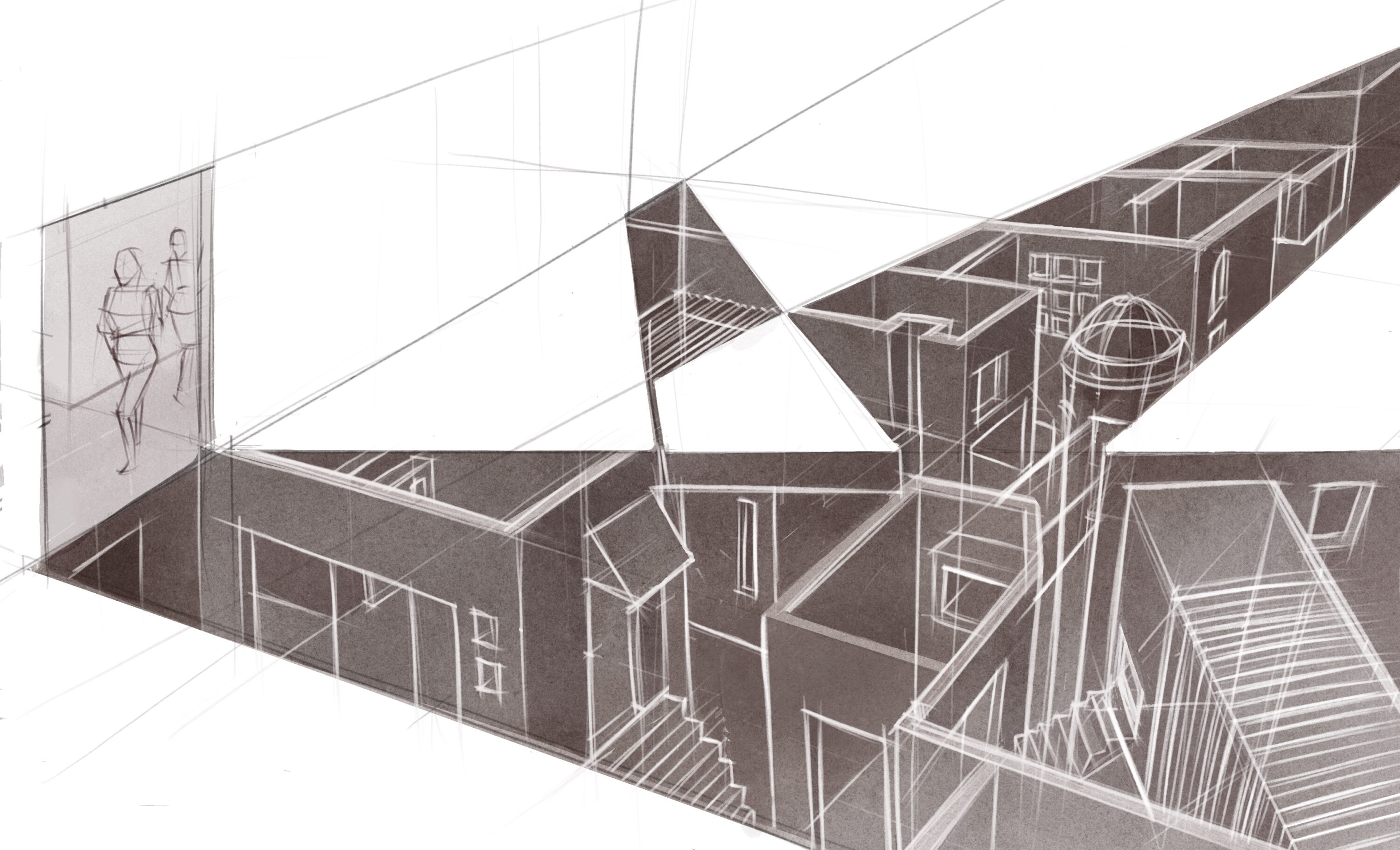
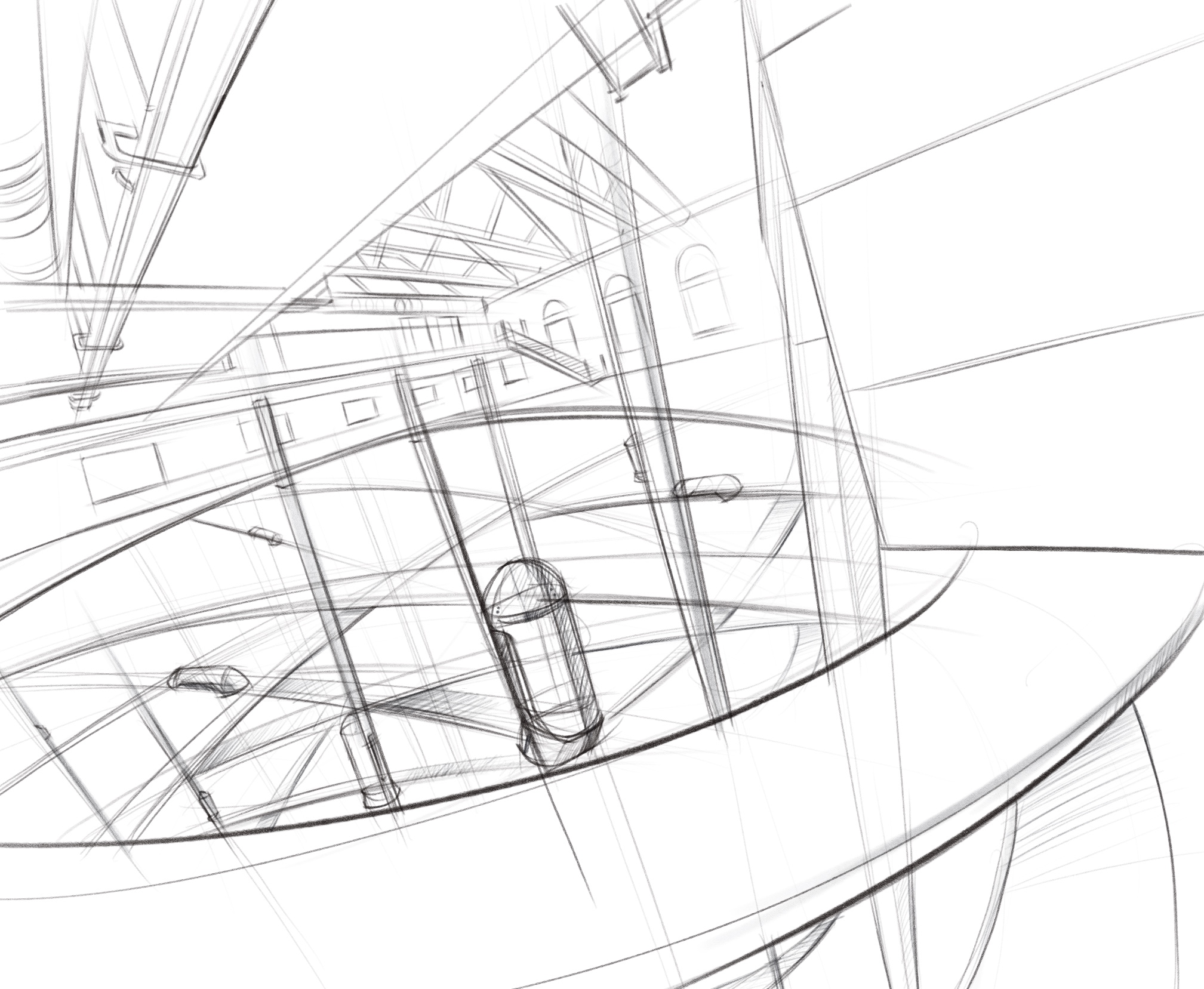
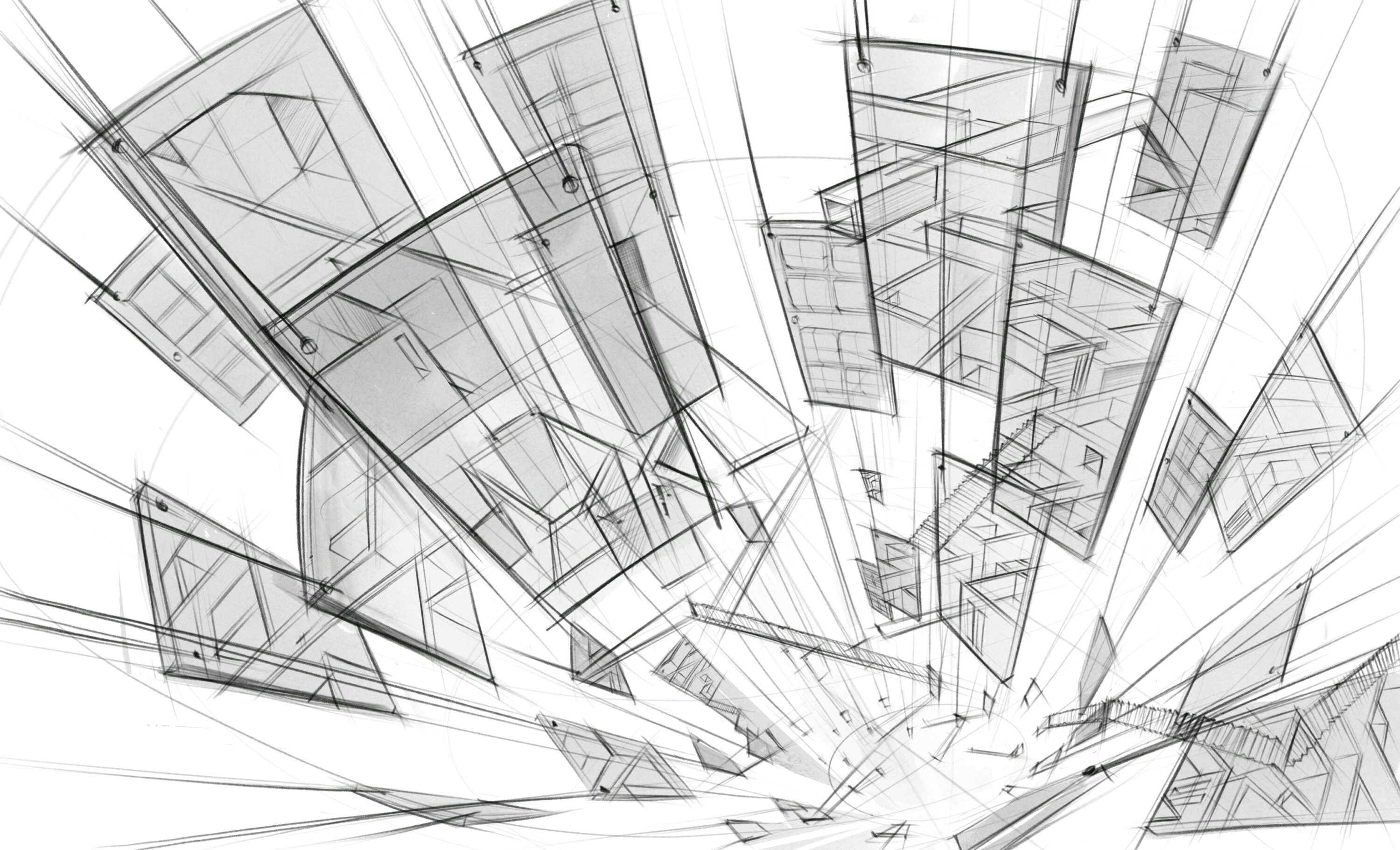
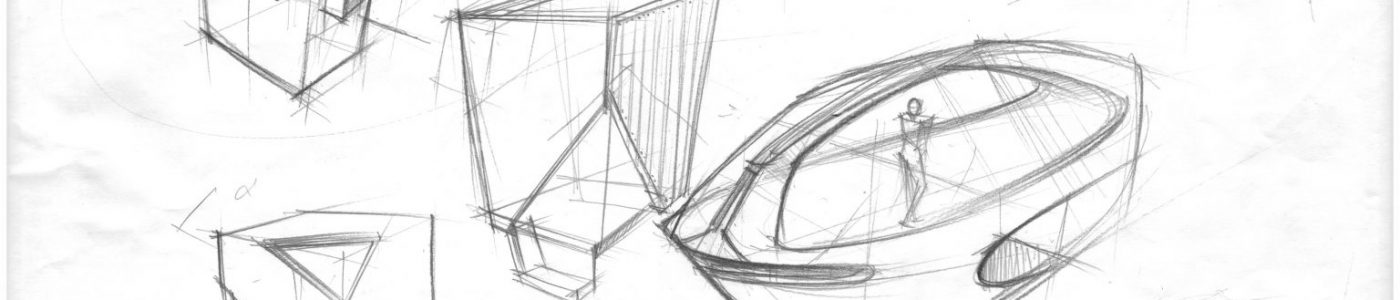
Primitive drawing practice is a warm up exercise that may as silly as they seems, however, it could really help you get sharp with your sketching and draw from imagination.
You may construct from a simple geomatric forms, make sure lines to converge to some vanishing point, play with your proportion as you go. It essentially create compositions, add extra ling weight at where it matters.
Objective
It is also called addition subtraction. Whole point of this exercise is to get you think proportion of a shape in perspective. You could think as architecture if you change the scale. The practice help to prepare you to draw more complex things and again,
The whole point of this practice is get your brain to think of mechanical perspective proportion and positioning your drawing, it creates your composition.